Bionic Experiments
Abstract
With the project “bionic experiments” a kind of reversed design process is tested, where not a design problem is the beginning of the journey, but the wish to make use of a principle from science for design. The principle of folding should be analyzed in such a way, that it can be translated to the language of design to find new applications, forms, or kind of material function. The goal is not to design a final product, but a conceptual translation of the essence of the bionic principle of folding to the language of design. Through exploratory methods several design experiments with different materials and tools help to get close to the bionic principle itself and to understand it as whole. The process of experimenting is documented in a weekly diary, which keeps an update of the design process, the findings and plans where to explore furhter. In the end the extracted principle is brought to an application or used as a tool for problem-solving.
Project start
KW 16 / FOLDING IN NATURE
Folding in nature is based on the principle that a concave fold always simultaneously arises with three convex folds. Because of this there is only a small amount of energy needed for the folding process and at the same time the folding gets an extremely high stability. Are several folds located in an area, they are interdependent. The individual folds can not be moved individually. One speaks of a kinematically coupled system.
To examine the convolution principle, exemplary folds from nature were translated in the material “paper” , to look at the folding and behaviour when used the folding principle in another medium as by nature.

ANALYSIING THE FOLDING PATTERNS OF A BEECH LEAF
The beech leaf complies to the folding pattern of kinematically coupled systems. It has only two folds, the upper fold and the lower fold. Through this principle of folding a large area can be accommodated in a very small space.

ANALYSING THE FOLDING PATTERN OF INSECT WINGS
The folding pattern of a n insect wing was built as a working prototype to analyse its folding mechanism also in motion – how does the pattern behave in motion? In which order the single areas do react?

The prototype, scratched from paper, was mounted to a servo, an i/o board and a motion sensor. The servo was programmed and controlled in such a way, that it reacted to motion, like in a real situation when the insect wants to flee when it detects an enemy. So through motion the paper prototype insect wing was unfolded, and flipped back to the folding position when the “enemy” was far enough away.
KW 16 / CONCLUSION
Further exploration is needed, looking to the working mechanisms of insect wings folding, techniques and patterns to understand the principle of folding in depth. Question: Where do the forces come, from that trigger the folding mechanism?
KW 17 / FOLDING WING MECHANISM OF THE DERMAPTERA (COMMON NAME: EARWIG)
The wingpackage of the Dermaptera is reinforced by elastic stresses in concentrated resilin areas (memoray points) and the center wing which is joint with the concave longitudinal fold to make it airworthy. The wings brought together have a smaller radius than 360 ° which makes them bistable. This mechanism is essential for the folding and unfolding at the same time. Due to the flexible resilin areas and the predetermined folding pattern, the wings can fold up automatically. Resilin is a rubber-like, elastic protein that can store mechanical energy.

MACRO OF THE WING FOLDING STRUCTURE
Just by the pattern how the wing is folded, a 10 times increase of the wing surface area is reached.
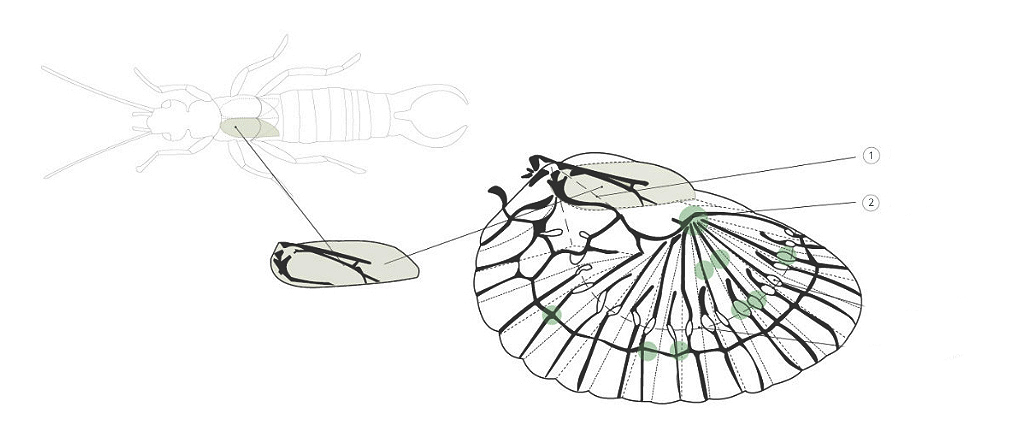
1) Longitudinal fold, concave
The crossing of the convex fold by the concave fold is a stiffening mechanism that counteracts a resilient voltage of the two ear panels.
2) Center wing joint
The center wing joint is the intersection of all radial and intercalary wires and connects the four major surfaces of the wing together.
Dashed Lines -Upper fold
Dotted Lines – Lower fold
Points, green – Resilin memory points
KW 17 / CONCLUSION
Further study of the wing structure and the mechanisms in detail . Comparison with other insect wings. Zoom in Zoom out of the center wing joint. Question: How does the joint work in detail, and what does it look like exactly?
KW 18 / INSECT WING STRUCTURES
For the wing construction two major types of joints are distinguished: the pleural wing joint and the center wing joint. The pleural joint functions as a gear shift and is relevant to the position of the wings during flight. It has in general three catch moments.
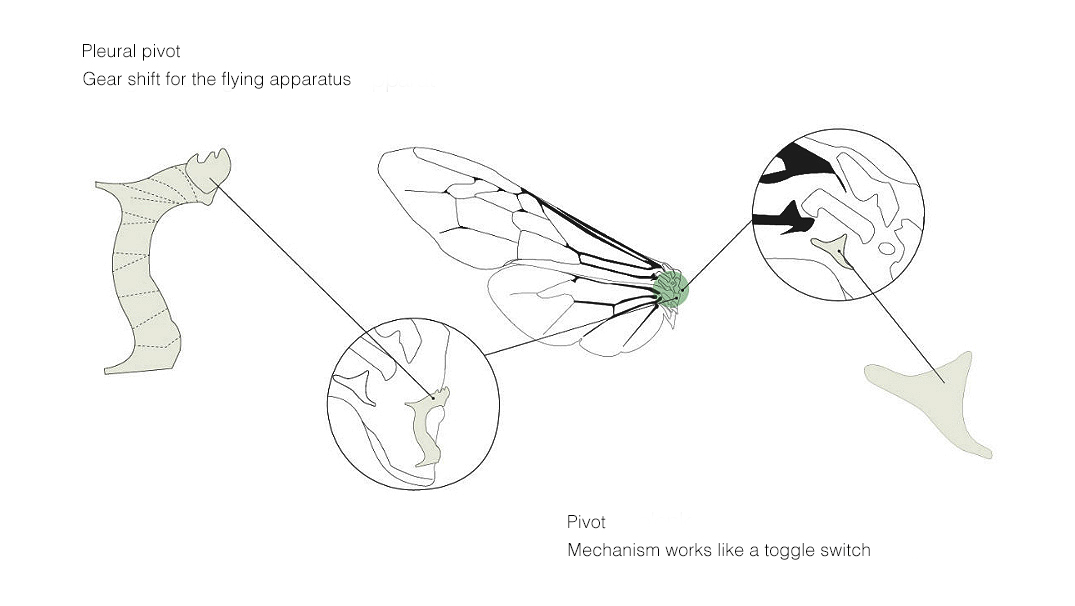

Due to the upward and downward movement of the wings the center wing joint is moved by muscles in the chest. So these muscles are causing the up and down of the attached wings.

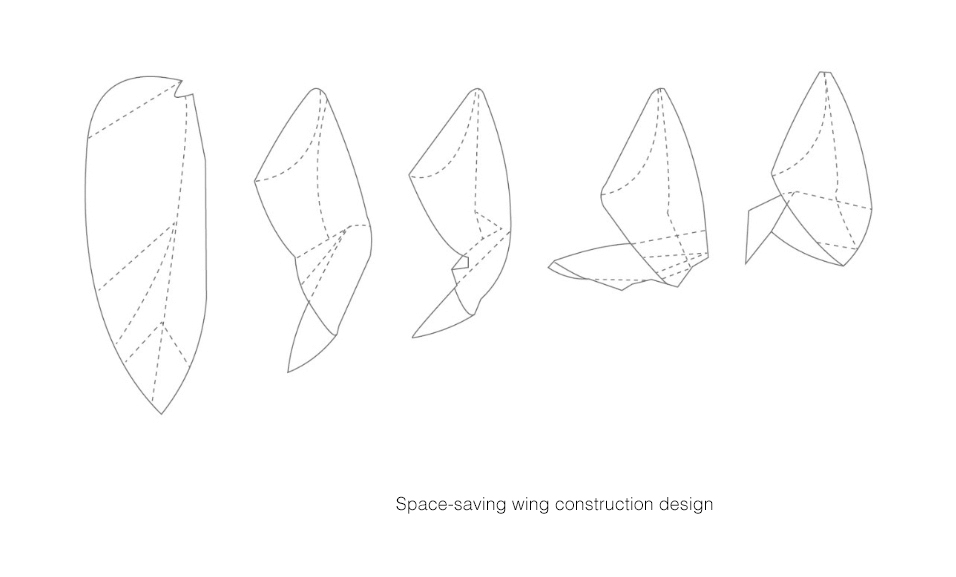
On the sides of the front and hind wings there is a pushbutton-type like mechanism that pairs both areas of the wing to fit together for flying. For wing-folding in general two folding patterns can be distinguisheda: just a simple and a double fold version.
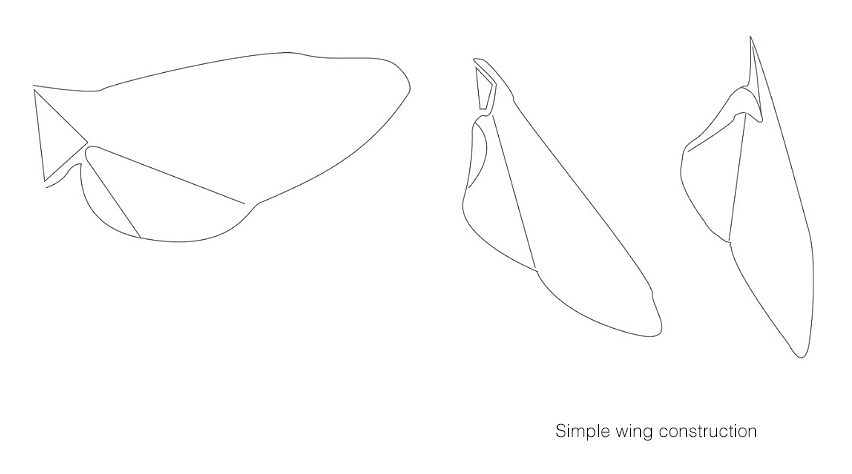
SIMPLE FOLDING PATTERN INSECT WING
Insects usually fold their wings in a simple or in a special space-saving principle.
KW 18 / CONCLUSION
Detachment of the principle of folding in own experiments. Question: How can I connect two surfaces in space just by folding? Is there a technique with little energy that allows connections that stiffen in case of a strong energy exposure in such a way that they can not be solved anymore?
KW 19 / FOLDING PROCESSES
Series of experiments and prototypes in paper, to design an own formal solutions of two-dimensional surfaces , by folding into three-dimensional objects. Through combination of upper and lower folds also complex folding patterns are possible. A fixation of parts of the figures can be achieved through slots and plugs.








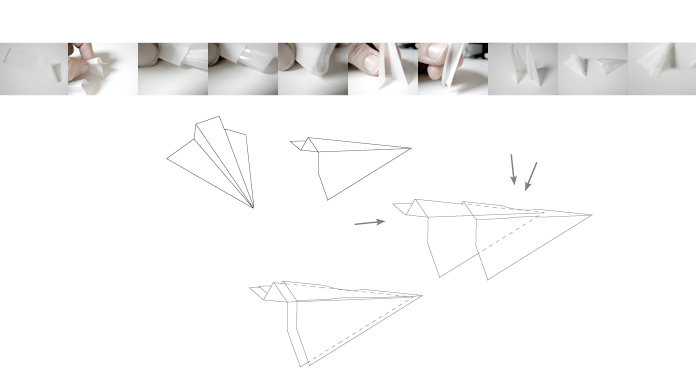
There are two states in paper inbetween which you can switch back and forth by taking advantage of the bistability of the folded object.

Figures with saddle surfaces result a certain direction in wrinkles very quickly, so that the material builds an internal stress on the objects and surfaces.

By moving the folding body of tubules always new characters and forms can be created, caused by the rubber thread inside the tubes. So the folding process surfaces can be studied very well.
KW 19 / CONCLUSION
Build the object of tubes in a larger arrangement and / or with more elements, look how it reacts. Where do the stresses of saddle surfaces come from in the experimnent of the paper body?
KW 20 / EVALUATION OF FORM STRUCTURES
By enlarging and detailing the wired tube body a variety of shapes, that was not in sight in the small model, became possible.
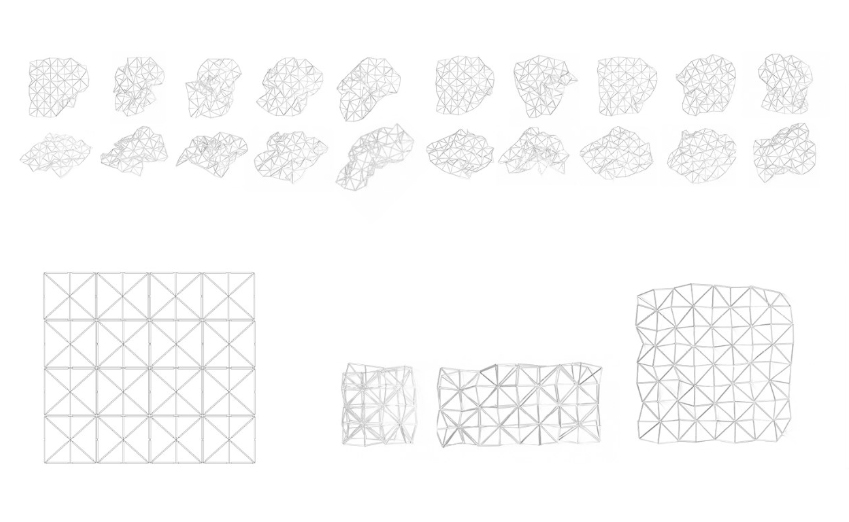

The body reacts to different force situations in a chaotic way and turns in various directions, thickens and opens up its structure. However, a systematic way can not be detected in establishing a relationship between forces and form responses.


The tubes of the object were joined by an elastic rubber band. In the areas where two or more tubes come together a node put in for intersection. There are two different types of nodes that have been applied : At the intersection of two tubes a double knot is used, at the intersection of three tubes a superimposed double knot is used. In the center of the pattern, where six tubes meet, a clamping node is used. By the manual knots different directions of the folding object caused by different tensions are the result.
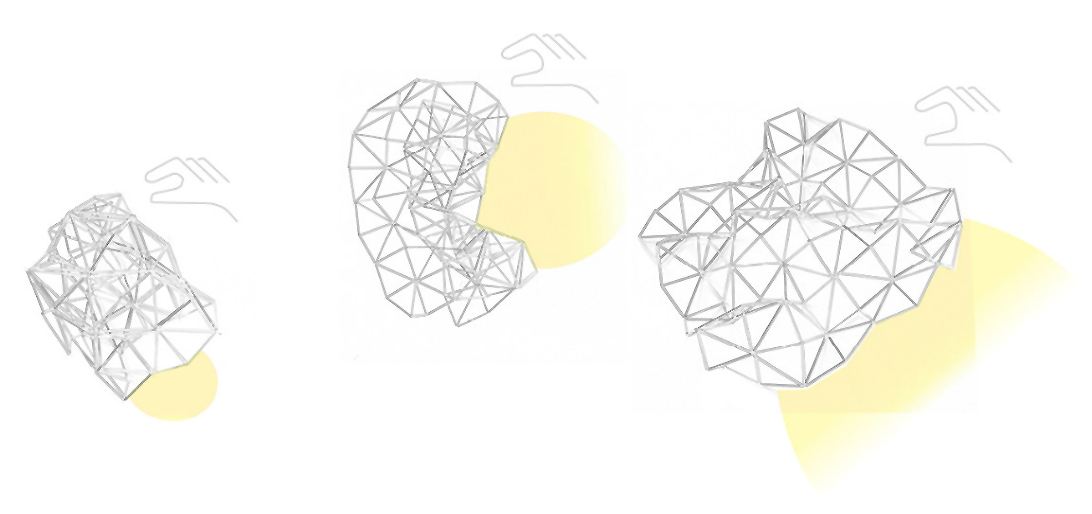
An application for the system of nodes could be a luminous object, for example in the dental field, which could be considered to different lighting states as the closely folding brings a directional or spot-like light and the opening of the folded pattern let the light be scattered. By squeezing and pulling the body, the intensity and scattering of the light can be controlled.
KW 20 / CONCLUSION
By applying forces to on one or two sides of the body it reacts in a chaotic, disorderly manner. Is there a way to develop an orderly, predictable method for folding and directing the body, means to control it? What is needed to achieve a uniform behaviour of the nodes ? Material research is needed on the topic of illumination – the object should not be a luminous object but an object that is illuminated.
KW 20 / THE GENERATIVE WAY OF FOLDING
STATUS REPORT
Folding techniques are used in nature to use little space as efficiently as possible and exploit it with a minimum of material to achieve an maximum of stability. The folds are based on the principle that a concave fold always simultaneously exists with three convex folds. Are several folds located in an area, they are always dependent on each other – this is called a kinematically coupled system.
Many types of insects fold their wings. They have two pairs of wings, one, the upper, which is strongly chitinized and protects the lower, the larger one, which is responsible for flying. By the folding technique of nature the airworthy wings can achieve a up to tenfold reduction of size.
Before flying, the wings are made airworthy by elastic stresses in resilin areas (resilin is a rubber-like elastic protein), and also stiffened by the center wing joint. The wing surfaces joined together a radius of not quite 360 ° so they can be in a bistable position. This mechanism for unfolding and folding is equally necessary, because the wings fold up automatically as a result of the flexible resilin points and the predetermined folding pattern.
Folding is also essential in design because by folding processes all two-dimensional surfaces turn into three-dimensional objects.
Based on the science of bionics, the wing folding techniques and mechanisms used in nature can be transmitted in folding other materials and so be converted into three-dimensional objects .
In researching the generative processes of folding, it is not the primary goal of creating a special object, but to analyze the actual flow of folding and reflect it for the design practice. Through experimental transformation rows of folding experiments the changes are considered separately from the surface to its form in each step and the forces and folding processes become visible.
KW 21 / EXPERIMENTS ON THE CONTROLLABILITY OF FOLDINGS
In this setting it should be analysed if and how the variation of individual components like material or the use of nodes, such as in the previously developed objects, can be controlled more efficiently so that changes in the shape can be reproduced repeatable.


When the object is made of paper, it has to be considered, that because of the bistabil reacting material, there is no way to control single surfaces. By this method of production, the body can not be controlled at all, because the wrinkles respond coherently. Paper remembers folds so that only two states fol folds are possible – upper and lower folds.
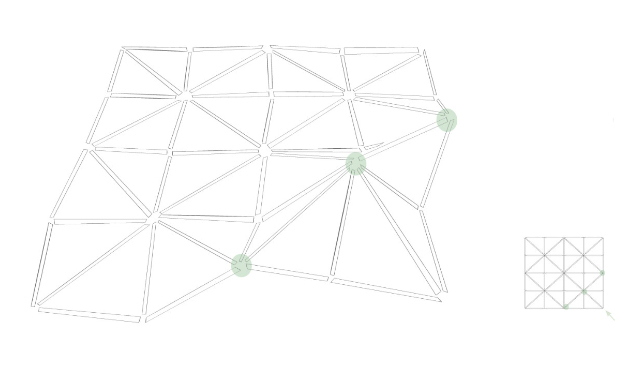

If the tubes of the object are connected by a flexible cord, they react when force is put to a corner, by moving up at the front, in the middle of the first square. Through this production way, the folding process of the body can be controlled only partially.


If the tubes of the object are connected by a solid line, they react when force is put on a corner, moving up in the middle first. By this method of production, the object can be easily controlled so that the first folding along the major diagonal line comes up first.


If surfaces are attached to the tubes and wires and forces are put to a corner, the tube elements associated with the surfaces first move up. By this method of production, the body can be controlled very well and it can be determined which areas should line up first.
KW 21 / CONCLUSION
Furthermore, focus on nodes is needed, even from complete strangers disciplines. How can a node be combined with other techniques? Is it possible to design a knot?
KW 22 / NODES AS LINKS
Nodes form reinforcements and are also transitions and connections between two or more elements. In combination with the topic of folding the type of knots for the design gets fundamental because it determines, depending on the material, the direction of the connected elements.

In the research field of protein folding within the science of biochemistry parallels can be produced to the topic . Each protein consists of long chains of amino acids and generally seeks to achieve a change in its extended shape. Proteins fold in order to achieve the most compact possible form. Protein folding denotes the process obtained by the proteins and their three-dimensional structure; each protein folds in the way and within its specific form that is always the same. During this folding some amino acids couples get closer together or get further apart. The structure specifies the function of a protein. Occuring misfolding of proteins can cause diseases such as Alzheimer and Parkinson.

By combining resilin areas in insect wings, the knowledge on the chaotic control of folded objects within this project and the investigation of the joints, a new kind of joint could be developed. The idea is still in a concept state to act as inspiration for various products or ideas. The joint consists of a hard core and forms, at each side, a hinge part which can elastically react and be combined with different diameters of tubes.

KW 22 / CONCLUSION
Concretization of two folding objects, according to different principles of nodes. Further elaboration of the joint is needed, thinking about setting options and limitations to angles and used materials. Time for mock-ups.
KW 23 / PRODUCT DEVELOPMENT IN THE LAB
Inspired by the principle of protein folding, folding objects out of paper with different principles of nodes are possible. By the nature of knotting and the resulting changes in direction it is possible to design abstract three-dimensional bodies and structures with a more sketchy character. Problematic is the translation in paper because the material responds too flexibly and does not stay within its shape especially in context of larger objects.
The original idea of a joint that connects a hard material with a soft one, is transferred to the design of an intelligent joint with three asymmetric arms. The joint is flexible and can change in almost all desired positions. The idea is that not only the arms of the joint should be mobile, it is desirable that the entire joint can move by itself. Alternative designs with a towing mechanisms are being considered. The first mock-up is made of plaster and only to develop a first idea of the concept and the form.
KW 23 / CONCLUSION
Elaborate the design principle of the joint further. How can the joint work with a completely new imaginary construction ? A more detailed model is needed. What application scenarios are conceivable for the joint?
KW 24 / CONSTRUCTION AND DESIGN PROCESSES
Several design techniques to control and adjust the joint radius are developed. The goal is to compare the positions and to evaluate. An alternative design idea is to work without internal joints or fixations. In the concept the main body of the joint could consist of two different plastic materials. The core would be made of roughened gray polypropylene, the hinge arms could be made of a translucent plastic based on polyethylene which is deformable.
First tests with a thermoplastic material, which can be deformed at low temperatures (about 60 °). The shape maintains when cooled down. When heat is supplied from outside, the shape changes too extreme because the whole form gets flexible. The desire is to make the plastic only in certain areas deformable so that it retains its originally shape.
Thoughts on the applicability of the development:
The joint could be useful in fields of temporary architecturak structures because the individual joints can be combined to a spatial structure. Here a further elaboration of the joints would be necessary.
Another application could be in the field of orthosis, because the joint can react identifiable and flexible enough to replace, for example, a plaster, because movements of the body part of the patient, could be set and controlled by the joints.
KW 24 / CONCLUSION
Seek solutions to let the thermoplastic material stay in the envisaged shape, because it gets to uncontrolled, especially at high temperatures. Maybe think only in subsites of thermoplastic. How can the joint be developed further?
KW 26 / DEVELOPING A MICRO-STRUCTURE
The intelligent joint could also be used for applications in the micron range, where it can be concatenated into an even finer, more convertible structure. Therefore a connector is needed, which couples the individual joints to larger surfaces.



The connectors serve as conductor of heat and can be used individually, as the joints themselves, and be controlled via an interface to change their shape.


KW 25 / EXPERIMENTS WITH THERMOPLASTS
Test series with a thermoplastic material which melts at low temperatures (about 60 °) and gets flexible. The thermoplastic material becomes transparent when heated in water and can be deformed. By cooling it gets a milky color and the material gets stiff again.
Test series heating though water
The material in the first test is made flexible with hot water.
Result: When the body receives heat from outside, the shape of the whole material changes too much because it is malleable. By heating in a water bath, the material is heated from the outside to the inside and can not hold the original form, it is uncontrollable. The desire is to make the plastic deformable – but the originally form should be kept.
Solution: The warming of the plastic should be done from inside out.
Series of experiments to heat by battery power
A resistance wire is worked into the thermoplastic material. This is becoming heated by a battery to radiate the heat throughout the material.
Result: The short circuit of a battery exposures a strong heat through the wire which warms up the plastic from inside out. It creates a melt primarily around the wire, that brings up enough flexibility for a deformation of the existing form of the joint to change without changing the whole form of it.

KW 25 / PRELIMINARY DESIGN
The joint is extremely flexible and can change in almost all desired positions. In order to keep the diversity of forms manageable, there are 10 different models that can be generated. For this purpose, the joint is placed on a plate which is connected to a computer. Through an interface a design can be choosen. If the choice is confirmed, the interface sends the information to the microchip which is inside the joint. The chip is connected through resistor wires and sensors with the articulated arms and determines which areas must be controlled for heating. The jont can then be moved in the predetermined position. Through some test series with resistance wire this concept could be tested. The final model was created in stereolithography and shows examples of three different states of the joint.
KW 27 / Result: EXAMBLAGE AS RESEARCH DESIGN CONCEPT
The scientific research referred to the planned, systematic search for new knowledge about the environment, human thoughts and human products. In this project hypotheses in the form of a design product are proved by experiments, observations and analysis and accompanyd by a consistent documentation. By extracting a principle from the science of bionics, and the translation into design and a visual space as well as the subsequent separation of individual components, the essence of the principle can be considered completely isolated. In the next step a stage of experimentation is necessary to test out things and to find out new comibinations. The word “Examblage”, is formed by the words “experimental” and “assemblage”. A “Examblage” is in design possible, because experimental methods and different forms of media can be combined. In this way, for example, an analytical method can be combined with practical methods to generate new knowledge for design. Design actions and their evaluation in experiments and the subsequent analysis as well as the evaluation of the knowledge is used in the design itself as a research process, called “Research through Design”.
In contrast to the approach of scientific research, which examines existing forms of logical statements and experiments, the design discipline develops intuitive, experimental and productive thinking as new forms of research for the design discipline. The initial situation is not a problem which is solved by the design, but a detachment from process until applications are found in the second step. This extended position can be a starting point to novel approaches for the designed relations of our future society.

